Worker Moves
There are important differences between how worker orders are executed between single player games and multi-player games. This analysis contrasts the differences between single player and Play by Email games — it should hold equally for other types of turn based multi-player games, but this has not been tested. For turn-less games all bets are off. The key point is a contrast between how worker jobs are executed. The game dynamics are very different between the two types of game and anybody switching from one type of game to the other should be aware of these differences.
Many players hold the following as a self-evident truth:
If you are going to make a road that is going to take three turns to complete then you should either assign one worker or three workers to the task. If you assign two workers then you will waste one worker turn (it will still take them two turns to complete the road).
Although true for a single player game, this is false for a multi-player game! Hopefully the analysis contained here will help players increase the flexibility of their worker gangs by shedding some light on the worker model use in Civilization III.
Please note that anybody who wants to get into this should already be familiar with Cracker’s analysis of worker orders. There’s no point in utilising this information without already understanding that.
I have been using Conquests to do these tests, but I’ve seen the same behaviour in Play the World and don’t expect that it will be any different in the vanilla version.
Important points
The analysis is a bit long in places so I wanted to get the important conclusions into the open at the start for those who just want to know the facts. For more detail continue to read the article.
The single most important point
In a single player game the dynamics are such that all workers in a stack will finish at exactly the same time even if this involves wasting worker effort.
In a multi-player game the dynamics are such that when enough worker effort has been put into a task then extra workers can be immediately re-assigned to other tasks.
Single and multi-player rules
- The Industrious trait adds 50% to the amount of work that is done per worker turn. In Civilization III vanilla and Play the World this figure was 100%.
- Do not stack workers making roads unless the turns saved to make the road is more important to you than wasted worker moves.
- If you want a road from A to B in a hurry on flat land then you should use six non-industrious workers or four industrious workers in a stack.
- There is a maximum worker stack size above which you will have workers who never get a chance to do any work. This depends on the terrain and the tasks, but is in any case very high. This maximum is never less than six workers and would normally be higher (four workers for an industrious tribe).
- There are ways to stack workers and slaves that provides a good compromise for wasted moves and earlier completion of worker jobs.
Multi-player rules
- Don’t be afraid to stack your workers in any number and feel free to have workers join other workers late.
- Do stack workers doing any task other than making a road so long as they can start working on the same turn they move onto the square.
Single player rules
- If you are going to add a worker late to a stack of workers (or just add the second worker) then you must calculate whether you will be better off or not. Think very carefully before doing this.
- If you change your mind about what workers in a stack should be doing you ought not to re-assign one or more of them unless you are totally desperate. You will complete the project much later and waste even more worker turns than if you let them complete the first project.
Play by Email Worker Moves—The simple Ancient era case
If we start in the ancient era with a non-industrious tribe then we can see that to build a road will take a base of 3 worker turns. That means of course that a single worker will take 3 turns to complete it, but how exactly does this work? (The numbers are the turns that things happen on.)
- Move the worker on to the tile
- Start road–-the first worker turn goes into the bucket.
- The second worker turn goes into the road.
- The third worker turn goes into the bucket and the road completes.
This means that the road will certainly be complete by the beginning of the next turn (turn 5), but would appear at some time during turn 4. What happens if we add a second worker?
- Move two workers on the tile.
- Start road-–the first worker turn goes into the bucket. Command the second worker to build a road and the bucket now contains two worker turns.
- The first worker adds a third move to the bucket and the road is complete. When the computer gets to check the second worker the road is already complete so this worker gets a turn.
The road is now complete a turn earlier, but also notice that the second worker is free on turn three to be moved to the next tile that needs a road or start a mine or irrigation project.
When you try this you will also see that the road is always complete by the time that the second worker arrives in your unit instruction cycle.
Forest clearing example
Here is an illustrated example to drive the point in further.
Note that the worker below will finish clearing the forest in four turns – this means that for a worker of this efficiency the work bucket is 4 turns deep. I have a nearby worker who will join the first worker next turn.
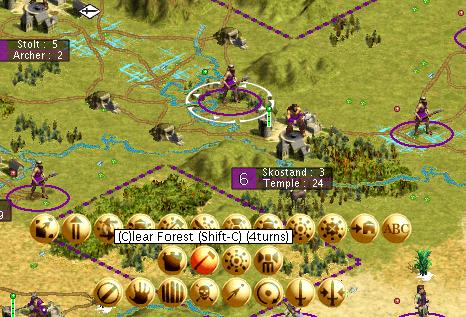
How many turns will it take to clear the forest and what will we be able to do with the workers when we complete it? Popular wisdom is that we will waste a worker turn when we add the second worker to do this. We will still clear the forest faster, but at the cost of wasting a worker turn where we could be doing something else. Let’s see if this is true.
Here is the next turn. The second worker has been moved across and as you can see the tree chopping will complete in 2 turns. Let’s add the second worker and see how it pans out.
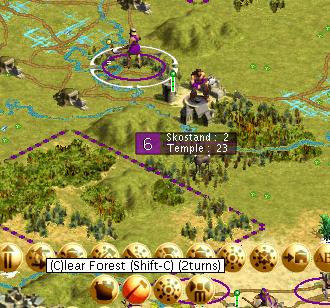
On the next turn we see that the forest is gone, our temple is a lot closer to completion and, most importantly, that only one worker turn was needed! The other worker is now free to start irrigating.
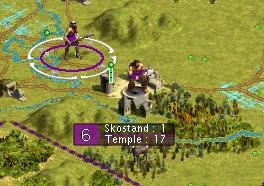
So, was there an advantage? Clearly there was. The work was finished earlier and we were able to start the irrigation earlier. Critically we also didn’t waste any worker turns. A total of 4 worker turns were used to chop down the forest (1 + 2 + 1). The turn sequence is laid out below.
- Move first worker to forest tile (note that there is already a road here). Instruct to chop down forest. The bucket (which is size four) now contains one worker turn.
- The first worker adds his move to the bucket. The bucket contains two worker turns. Move the second worker to the forest and instruct him to chop it down. There are now three worker turns in the bucket.
- The first worker adds his move to the bucket. The bucket is now full and we harvest the shield. The second worker is now free to do something else as his move was not needed to clear the forest.
Worker moves in a Single Player game
The game dynamics are different for single player games. This is what happens when we chop down a forest and bring a worker in a turn late to help us.
- The first worker starts work. His move is put in the bucket.
- The second worker joins him. His move is put in the bucket. The first workers turn will be put in the bucket later.
- Both workers work on it. Here both worker turns are to be put in the bucket after our turn sequence.
- The forest is clear and we can re-assign the workers.
So what happened? If we add up the number of worker turns of effort that were used we can see that this time it is 1 + 2 + 2 = 5! How does this happen? It seems that the game works out when to do things in a completely different way.
In a Play by Email game the workers put their work into the bucket either when they are first assigned to do a task, or at the end of the next turn. In a Play by Email game the next unit of work is put in the bucket during the inter-turn.
Here are some screen shots of the above scenario. It is played in Conquests with a non-industrious tribe.
Turn 1

In the above picture we are just about to assign the worker to start chopping down the forest. We can see that there are four worker turns. There is a second worker ready to join in next turn.
Turn 2
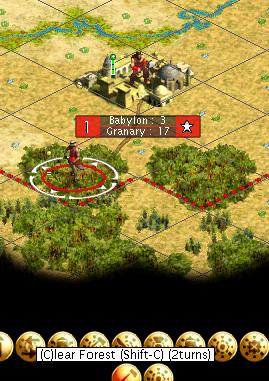
The second worker joins in and we are told that there are 2 worker turns left. So far it is exactly the same as the multi-player version.
Turn 3
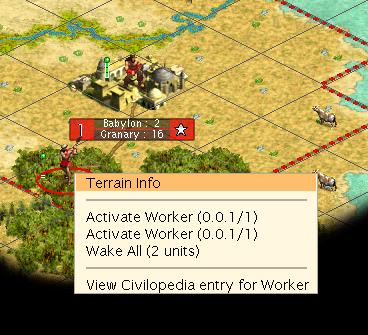
In our next turn we do not see the forest cleared. Why? Well, the two workers haven’t had their go yet. In the Play by Email version the next worker turns were done during the inter-turn. In a single player game the worker turns are now done later.
This difference is critical. Because the workers go last and not first the game cannot hand us the worker turn that would get wasted.
Turn 4
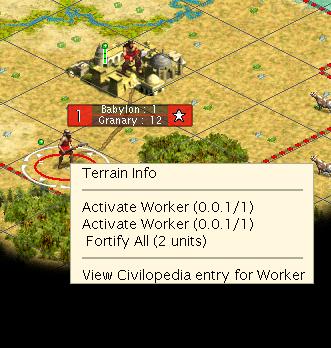
Here at the beginning of the next turn the forest is clear, but the extra worker turn we put into it is clearly gone and wasted. We can’t carry it over.
Regaining lost Single Player moves
There are two ways we can try to do this. We can either arrange for the worker to arrive one turn earlier or later so that there is always an even number of turns to deposit in our bucket or we can cancel one of the worker turns on the last turn. These two cases are shown below.
Remember though that you will always waste moves when building a road. For a full analysis of this see the next section.
Building a road and arriving late
We’re going to see what happens if we turn up late when building a road. Hopefully we can get the road completed faster and not lost a worker move in the rounding.
Turn 1
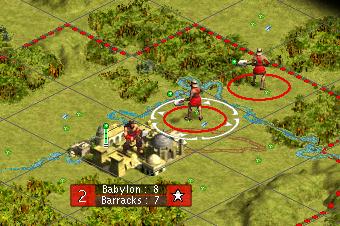
We have two workers. The highlighted worker is going to move NE and join the worker on that tile.
The other worker is instructed to start the road.
Turn 2
The second worker has now joined the first we tell him to build road.
Turn 3
The road is complete and we have both workers available to instruct.
Building a road and re-assign
What does this mean? We are going to try to see what happens when we put the two workers to making a road but instead of allowing the final worker turn to be wasted we’re going to re-assign that worker to irrigation. Here’s how it works out.
Turn 1
We have two workers and we tell them both to start building a road. We know it will only take three turns, but we also know that we can re-assign a worker just before it completes so we’re not worried.
Turn 2
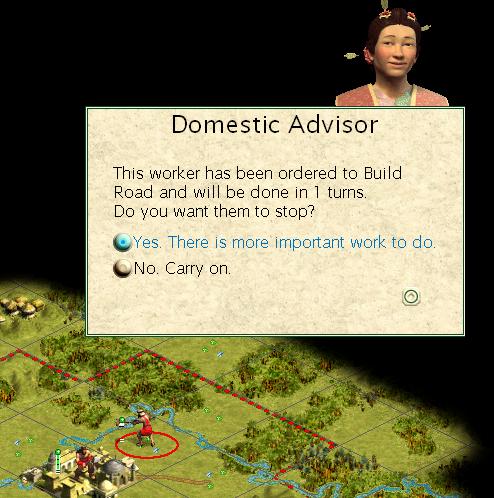
We have two worker turns in our bucket but don’t want to waste the fourth turn that allowing both to continue would do.
We select one of the workers and cancel their instruction.
Turn 3
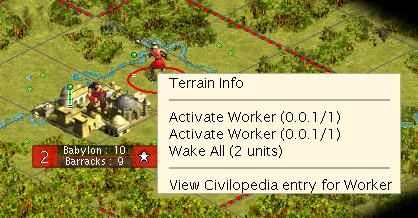
Hold on. We have one worker irrigating, but the other was still making a road last turn. Shouldn’t the road be finished and the road building worker be back under our control?
Turn 4
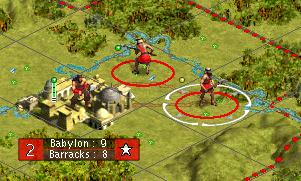
Finally the road is done and we can move the worker who wasn’t irrigating away.
So what happened here? As far as wasted worker moves go this seems to be complete disaster!
What it looks like is happening is that cancelling one of the workers cancels both their moves for that turn. This is why the road turns up even later. The moral of this story is don’t change your mind!
Note that if we cancel both and start one making a road and the other irrigating then it gets even worse. The one building a road will still take three full turns to do so.
As far as regaining lost worker moves it seems it can’t be done. If you make a mistake and don’t stack workers in an exact multiple of the number of turns to complete the job then you will waste extra worker moves.
How fast is too fast?
Is there a limit to the number of workers we can utilise on a project? Yes there is. If our goal is to build a road from point A to point B then there is an upper limit to the number of workers that can be usefully put to this task. Here’s how to work it out:
- We take a stack of 2 workers and move them on to the next tile we want to road.
- Tell both to start the road. They get their shovels and commence work.
- One worker finishes the job, the other is now free and we move him on a tile.
- The next worker is now free so we move him on a tile. We instruct the first worker to start a road on the new tile.
- We instruct the second worker to start a road.
- Both workers are finished and we’re back at step 1. We can move them on a tile.
If we add one worker then this happens:
- We take a stack of 3 workers and move them on to the next tile we want to road.
- We instruct them all to start building a road. The road is done.
- We move them all to the next tile. This is the same as step 1 above.
This is pretty good, but can it be improved on? Let’s see about 4 workers:
- We take our 4 workers and move them to the first tile.
- We instruct the first 3 to build a road and it’s done. The final worker moves on a tile.
- The worker on the second tile is told to road. We move the other three onto that tile.
- We instruct the first two of the new workers to build a road and it is done. The other two move on.
- The two workers on the new tile are told to road. The other two workers join them.
- One of the workers will complete the road. The other three workers move on a tile.
- We now make sure that we utilise the three workers in a stack on the new tile first. Tell them all to build a road and it completes. The fourth worker on the older tile can move through their tile on to a new tile. This is exactly the same position as we had in step 2 above.
We can carry this on to any number of workers we want. At six workers we get this:
- We move the six workers to their new tile.
- The first three build a road, the next three move on.
- The three on the new tile build a road and the three who have just finished move through to a new tile.
You are now back in the same position as turn 2. Nice and easy again. But critically what happens when you add a seventh worker?
- The first three workers complete the road. The other four workers move on.
- The first three workers on the new tile complete that road. The three on the previous tile move through to a new tile. The fourth unit on the just completed tile moves on.
From here we have the same sequence as the six worker example except that we have an extra unit who always moves onto a new tile. We don’t get any work out of one worker every turn as he’s always moving to a new tile. This is clearly a waste of a perfectly good worker who should be doing something else.
If we were irrigating whilst we were going along then the number of workers we would need before we started to waste worker turns would be increased, but in any case there is an upper limit.
Are there any circumstances that change this? Indeed there are. If you look at a stack of workers adding rails where there is already roads then you can go through the above exercise and see that you always use as many workers as you have available. This is because the completed rail road has zero move cost and the workers will have the opportunity to work after they move onto a tile with roads on it.
So we can see how stacks work, but how efficient are they?
A single worker to road a tile takes 4 turns to do so (one to move there and three to build the road). The stack of two workers took a total of 5 worker turns to do the same task (move one worker, move the second worker and it still takes three ‘moves’ to complete the road). This means that if you move a stack of 2 workers you waste one worker move. Similarly if you move a stack of three workers then the same road takes a total of six worker moves.
This means that you should only stack workers making roads where the saved turns to get the road completed earlier are more important than the wasted worker moves!
Don’t forget though that stacking workers irrigating or mining (or any other task) is just as efficient as a single worker so long as the worker is able to start working as soon as they enter the tile. Normally this means that there must already be a road or rails on the tile.
There is another small point to consider here too. If you look at our example of more than three workers stacked to build a road you will see that the road completes even faster, but we never waste more than three worker moves per tile of road (this is on flat terrain anyway). If you really need a road quickly then you should have a stack of six workers doing it.
Factors on worker speed
Governments have an effect on the speed of workers as do some technologies. These are the normal factors in Conquests:
- Anarchy—work half speed.
- Democracy—work at 1½ times speed.
- Fascism—work at double speed.
- Replaceable parts—doubles worker speed.
- Slaves work at half speed.
- Clearly we can’t ignore the Industrious trait in this analysis. It turns out that this allows workers to get a 50% bonus on their speed in Conquests, but a 100% improvement in speed for vanilla Civilization and Play the World.
The Calculations
The editor makes it clear that each worker job has a bucket made up of units of worker turns. We’ll call these base worker turns (BWT). On the standard rule set an ancient era worker for a non-industrious tribe will do two BWT per actual game turn (GT). For an industrious trait this changes to three.
The following table shows the worker jobs and their BWT:
| Job | BWT |
|---|---|
| Build road | 6 |
| Irrigate | 8 |
| Mine | 12 |
| Fortress | 16 |
| Barricade | 16 (N/A for Vanilla & PtW) |
| Railroad | 12 |
| Plant forest | 18 |
| Clear forest | 4 (Vanilla & PtW are 5) |
| Clear wetlands | 16 |
| Clear damage | 24 |
The above number won’t give you the full amount of work that needs to be done. In order to calculate the size of ‘bucket’ that must be filled the base BWT is multiplied up by the movement penalty on the tile.
So, building a road on grassland requires 6 BWT (1 x 6), for hills 12 BWT (2 x 6) and for a mountain 18 BWT (3 x 6). Normally these will take 3, 6 and 9 turns respectively for a non-industrious tribe (ignoring other government & technology factors above) and 2, 4 and 6 turns for an industrious tribe.
Ganging together a worker and a slave
From this we can predict what will happen when we team a worker with a slave to make a road.
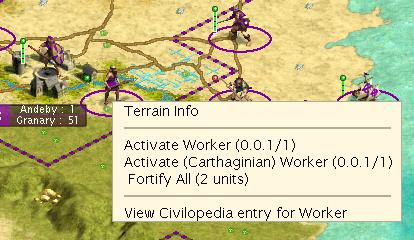
The prediction is that a worker and a slave (from a non-industrious tribe) ganged up above should be able to build a road on this flood land tile in 2 turns ([2 + 1] + [2 + 1] = 6 BWT). Below is what happened (this is actually the next turn as both the worker and slave completed their task during the inter-turn).
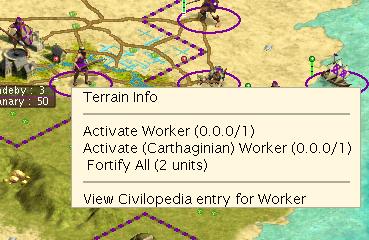
Exactly as predicted the road is complete and we’ve used the turns of both the worker and slave.
Final illustration
This simply shows a stack of slaves who have been working on improvements. They were all working on mining the tile in question, but have now finished. As you can see, some of their next moves were consumed, but not all.
Remember though, this will only work for multi-player games!






