Collatz
We've done a variation on this puzzle before, but then of course there wasn't a cool XKCD comic.
The sequence can be defined in this way:
n -> n/2 (n is even) n -> 3n + 1 (n is odd)
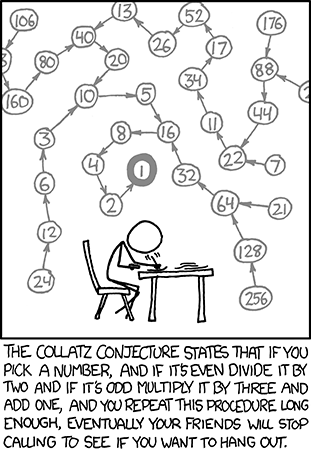
And the conjecture is that no matter what positive starting integer you start from the sequence of numbers will always reach one. I.e., starting from 13 gives the following sequence:
13 40 20 10 5 16 8 4 2 1
For odd numbers we do the following: 3n + 1, where n is the current integer in the sequence. Is the three arbitrary, or does the conjecture not work for other odd values? I.e. if we take the formula as k.n + 1 does every positive integer still eventually reduce to 1?
Write a program that checks to see if the conjecture holds for k = 5
Three and five are just two values of course.
Check to see if the conjecture holds for other odd values of k
How far can you check? What bounds are you putting on the calculations? And, how many of your friends have called whilst you've been doing it?
